Conways Pattern

Conway's Game of Life X Audio-driven pattern generator

BACKGROUND

The aim of this project was to develop an interactive pattern generator which was both original and perceivably appealing. In order to achieve this the programme of Conway’s Game of Life was used to produce the visual display. The Game of Life is a simple computer model, which simulates population behaviour. It was created by the mathematician J.H. Conway in the 1970s.

In order to create an interactive version of Conway’s simulation, a microphone was implemented with the purpose of providing data, namely the decibel level of a room, for the program to use as a variable in modifying the rate of generations passing.

Not only did the game demonstrate how incredible complexity could arise from a few fundamental laws, but it also proved useful in mimicking systems concerned with the behaviour of populations (i.e. overcrowding, under population and reproduction).

Location /

Maastricht University

Role /

Project design and lead

Purpose/

Project period

Year /

2014

Team/

Sven Cleeves, Rachael Hall,Oliver Tunnacliffe, Nina Troppmair, Mischa-Alexander Ansari,Lexanne Keulemans, Jillian Loree, Janneke Mes,Emily Sellman,Darja Stoeva

Source: Sam Twidale: https://experiments.withgoogle.com/conway-game-of-life

METHOD & THEORY

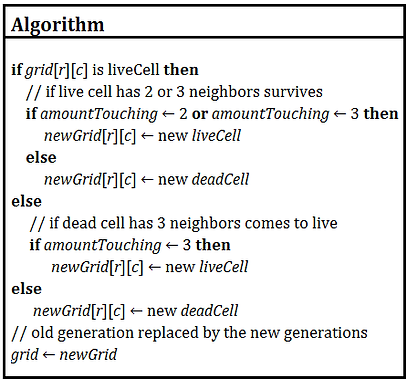
Conway’s Game Of Life is a cellular-automation zero player game. The game is played on an infinite grid of square cells and its evolution is only determined by it’s initial states. The initial grid consists of cells, which can either be dead or alive. By these simple rules, the generations can be mathematically simulated.

Any live cell with fewer than two live neighbours dies, as if by underpopulation.
Any live cell with two or three live neighbours lives on to the next generation.
Any live cell with more than three live neighbours dies, as if by overpopulation.
Any dead cell with exactly three live neighbours becomes a live cell, as if by reproduction.

These rules, which compare the behaviour of the automaton to real life, can be condensed into the following:

Any live cell with two or three live neighbours survives.
Any dead cell with three live neighbours becomes a live cell.
All other live cells die in the next generation. Similarly, all other dead cells stay dead.

In every generation, these rules are simultaneously applied to all cells in the grid, which causes the pattern to change in a predetermined manner at every generation. Some patterns can stabilise, this is caused by survival of certain cells without any cells dying or being born in it’s proximity.

Below are show samples of the pseudo code used to develop the programme.

The following images demonstrate some of the patterns generated by the programme. Soon I will add further code to GitHub and add a gif of the programme working.